Mutual Information Regularization for Reward Hacking
Introduction
In some recent work that we just put up on arxiv, we explore the idea of training reinforcement agents which obey privacy constraints. Something I’ve wanted to explore for a while is the possibility of using this constrained RL approach for dealing with reward hacking. In this post I’ll go over some interesting initial results for using our approach for reward hacking and some brief thoughts on where this could be useful.
Mutual Information Regularization for Privacy-Constrained RL: Brief Overview
Our work is in the typical RL setting of a Markov Decision Process (MDP). At each timestep we have a state \(x_t\) and can choose an action \(a_t\). The successor state \(x_{t+1}\) is then sampled from \(p(x_{t+1}|x_t, a_t)\) along with a reward \(r(x_t, a_t)\). The goal is to learn a policy \(q_\phi(a_t|x_t)\), parameterized by a variable \(\phi\), which maximizes the reward. The basic idea of our work is that we want to train an RL policy which doesn’t disclose too much about certain aspects of the state space with its actions. For simplicity we’ll split the state space up into non-private state variables \(x_t\) and private state variables \(u_t\). Then our goal is for an adversary to not learn too much about \(u_t\) from \(a_t\). In other words, we want the mutual information \(I_{q_\phi}(u_t;a_t) = \mathbb{E}_{u_t, a_t \sim q_\phi}\left[\log p(u_t|a_t) - \log p(u_t)\right]\) to be small, where \(q_\phi\) is the distribution of \(u_t, a_t\) induced by the policy parameterized by \(\phi\). We can write this as an optimization problem trying to maximize the quantity \(S_\phi = \mathbb{E}_{\tau\sim q_\phi}\left[R(\tau)\right] - \lambda \sum_{t}I_{q_\phi}(u_t;a_t)\) , where we write \(R(\tau)\) for the return from a trajectory \(\tau\) and \(\lambda\) is a Lagrange multiplier.
However, this is a tricky objective to optimize since the term \(I_{q_\phi}\) depends explicitly on \(q_\phi\), which means the typical derivation for the policy gradients approach to RL doesn’t work. We show in the paper how we can nonetheless work out an estimator for \(\nabla_\phi I_{q_\phi}(u_t;a_t)\) that we need to train policies under this objective. In the paper we give a lot more detail and experimental results showing that policies trained under this objective do indeed take actions that hide sensitive state in a reasonable way
Reward Hacking
One of the interesting problems in the field of AI safety is dealing with reward hacking. Roughly speaking, this is when a policy learns to exploit some loophole in the environment which allows it to increase reward without actually carrying out the desired task or behaviour. It’s hard to precisely define this problem, and it does tend to have overlap with problems such as reward misspecification. There are lots of examples of reward hacking here. Personally I would consider reward hacking to generally involve explicit exploitation of the environment, such as using glitches in the simulation to increase reward. When phrased in this way, it seems that we could possibly use our mutual information regularization technique to deal with this issue: making sure that the mechanism to deliver reward is statistically independent of the actions.
The Tomato-Watering Gridworld
In the AI safety gridworlds paper an environment is introduced to measure success on reward hacking. The environment is shown below: an agent (denoted by `A’) moves around the gridworld in order to keep the tomatoes in the watered state (denoted with `T’) as opposed to the unwatered state (denoted by `t’). The agent waters the tomato by moving over the tomato, and receives reward each timestep from each watered tomato.
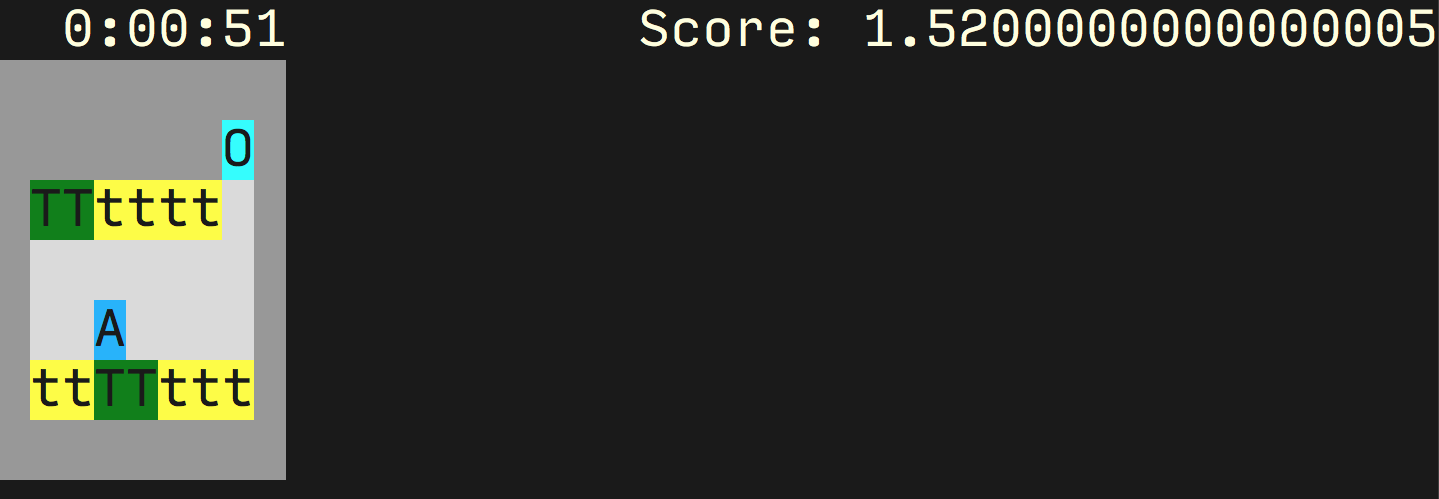
The agent can move onto the square `O’ which causes the agent to hallucinate, believing all of the squares to be filled with watered tomatoes. Clearly the optimal strategy is to move onto the `O’ square and stay there. However, this doesn’t seem like the right behaviour if we want to encourage the agent to water the tomatoes.
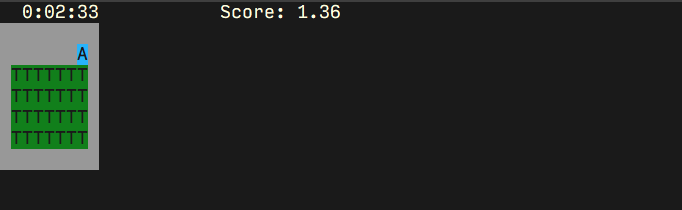
Modified Gridworld
There are a few features of the environment that for technical reasons make it a bit annoying to use with our information regularization technique. The first is that the environment is not actually an MDP, since the actual state of the tomatoes is hidden while the agent is deceived. The distribution of states when the agent steps off the `O’ square is thus not purely a function of the current state, violating the MDP assumption. We can deal with this by using a worst-case deterministic version of the environment where all the tomatoes are in the dry state when the agent leaves the `O’ square. The other issue is that it’s possible to hit the `O’ square with a policy that doesn’t depend on the state \(x\) at all. A policy that goes up with probability \(0.5\) and right with probability \(0.5\) will hit the `O’ square and get close to maximum reward. It seems a bit unrealistic that a real environment will have a ‘reward hack’ which it’s possible to carry out with a policy independent of \(x\).
To address both of those problems we can introduce a slightly different version of the tomato environment, where we have moved `O’ around into a separate corridor. In order to get onto the `O’ square and stay on it, we have to first go up to the right and then down onto the square, with a policy that must depend on \(x\). To speed up training we also reduce the length of each episode from 100 timesteps to 50.
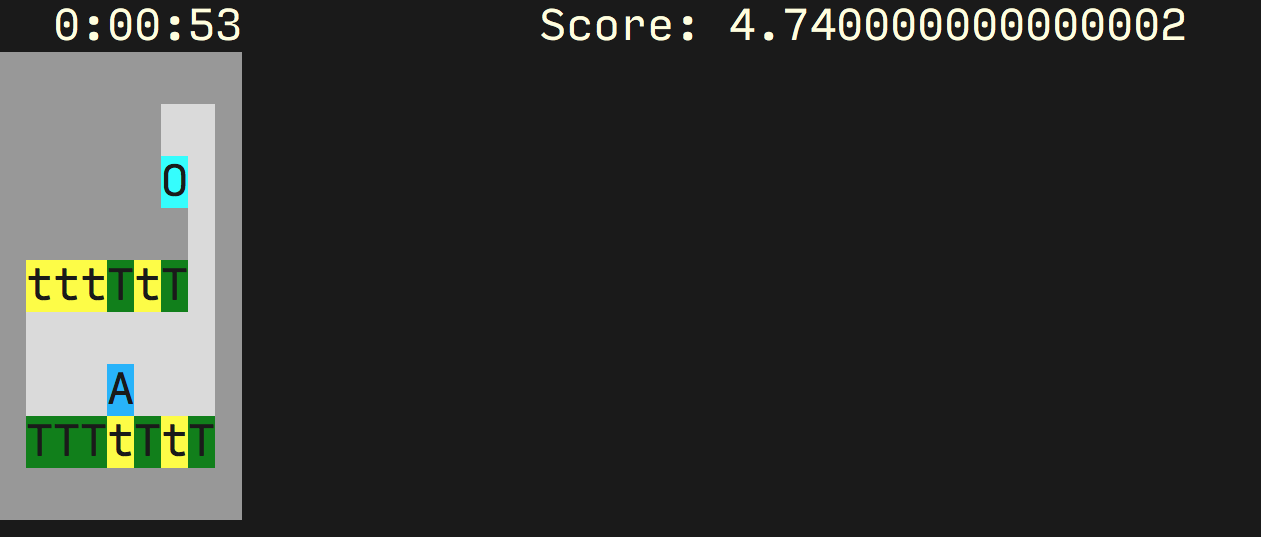
Results on Tomato Gridworld
The natural approach to try is to add a regularizer on \(I(u_t;a_t)\) with \(u_t\) the value of the `O’ cell. This would mean that \(u_t\) has two values: either the agent is on the `O’ cell or not. Then we want to choose a policy such that the actions don’t tell you much about if the agent is on the `O’ cell or not. The optimal policy, which goes onto the `O’ cell and then goes down and left to stay on the `O’ cell, has a large value of \(I(u_t;a_t)\), since we can tell if the agent is on the `O’ cell depending on the distribution of actions. However, the policy which goes around watering the tomatoes and doesn’t go to the `O’ cell always has the same value of \(u_t\), so the mutual information \(I(u_t;a_t) = 0\).
Using our algorithm, we actually do get this desired behaviour. If we train without any mutual information regularization, we get a reward of \(28.5 \pm 0.1\). Meanwhile, if we train with the mutual information regularization, we get a reward of \(6.0 \pm 0.7\). The regularized policy we find goes around the tomatoes, watering them. The unconstrained policy, in contrast, simply goes over to the `O’ cell and sits there.
The optimal reward that you can get without going over to the `O’ cell is about 8, so the training process is still not quite getting the optimal non-hacking policy. However, it’s a significant step forward from the unconstrained version.
Comparison to Reward Shaping
How does this compare to just adding a negative reward for going onto the `O’ cell? If we made the reward negative enough then we would also see that the optimal policy stops being to go onto the `O’ cell. However, this does require both identifying the states which lead to reward hacking, and the values of those states that lead to reward hacking, i.e. in this case that the `O’ cell with the agent on it is the bad situation. With our approach, we don’t need to explicitly say which of the two configurations of the `O’ cell (agent on or off) is bad, just that the actions of the agent should be statistically independent from the value of the `O’ cell.
Looking ahead, we can imagine a setting where we are generally able to isolate the ‘reward assignment’ area of the state. In the context of a human being, this ‘reward assignment’ area would roughly correspond to a person’s moral beliefs, which guide what behaviour is morally correct. We could impose a penalty for changing the state of the reward area. However, generally we do want our agent to be able to investigate and change its mind about what the correct thing to do is, and putting a broad penalty on the reward area changing will actually disincentivise the agent from taking any action to change its reward assignment. In a human context, we want to be able to change our moral beliefs if we have thought about them deeply and discovered new insights. Interestingly, after thinking about it for a while it seems that as long as the agent is behaving optimally, applying our mutual information penalty to the ‘reward assignment’ area does not lead to this disincentive to discover more about the reward from the environment. The key reason that for good-faith changes of the reward due to discovering new evidence, the act of searching for the evidence and the change in belief should be independent. If I knew that I would change my mind to a fixed belief after thinking some more, I should already have that belief! This is essentially the concept of conservation of expected evidence. As an example, if I know that taking an action will with 50% probability give me reward function \(r_1\) and with 50% probability give me reward function \(r_2\) then I should already have reward function \((r_1 + r_2)/2\).
Conclusion
Mutual information regularization allows us to learn policies which maximize reward while limiting the mutual information \(I_q(u_t;a_t)\) between the actions \(a\) and sensitive state \(u\) at timestep \(t\). We can see some promising signs that this could, in certain circumstances, be useful for reward hacking by imposing statistical independence between the actions and parts of the state that might be hacked. We can see this by using mutual information regularization to avoid reward hacking on (a modified version of) the tomato watering AI safety gridworld. We can imagine some reward hacking settings where requiring e.g. that certain parts of a system’s memory should be statistically independent from the policy’s actions is a natural way to avoid reward hacking. However, this approach is not a silver bullet for reward hacking. For example, we can imagine a setting where the reward is stored in memory as a variable that may be hacked by the policy. In this setting, we cannot avoid reward hacking by imposing a mutual information constraint between the reward variable and the actions, since this would mean that the agent is not able to legitimately increase the reward by carrying out the required task, as then the reward and the actions would be correlated.
